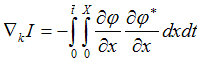Пусть на
конечный момент времени имеем данные измерений, насчитанные по модели с
известным коэффициентом турбулентной диффузии kист
в дальнейшем считаем что значение коэффициента нам не известно и решаем
задачу его идентификации в направлении следующего градиента функционала:
|
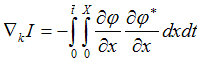 |
(1) |
Истинное
значение k ищется итерационно по формуле:
|
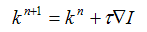 |
(2) |
В
результате работы процедуры коэффициент турбулентной диффузии хорошо
восстанавливается вне зависимости от его значения:
|
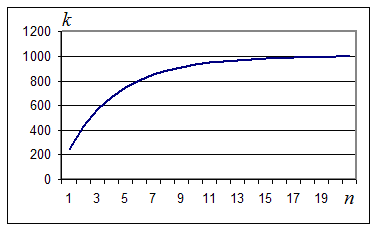 |
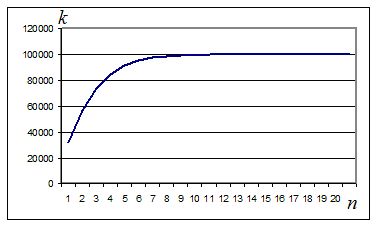
Рисунок
1. Восстановление истинного значения коэффициента турбулентной
диффузии в процессе итераций.
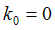 |
|
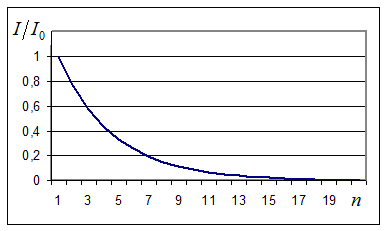 |
Рисунок
2. Падение нормированного значения функционала качества прогноза в
зависимости от номера итерации. |
|
 |
Рисунок
3. Восстановление истинного значения
коэффициента турбулентной диффузии в процессе итераций. |
|
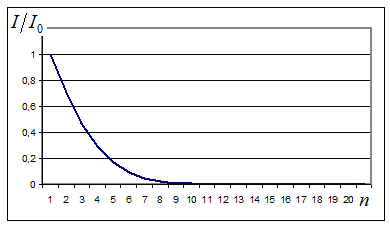 |
Рисунок
4. Падение нормированного значения
функционала качества прогноза в зависимости от номера итерации. |
|