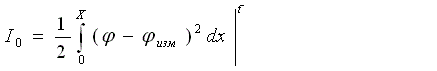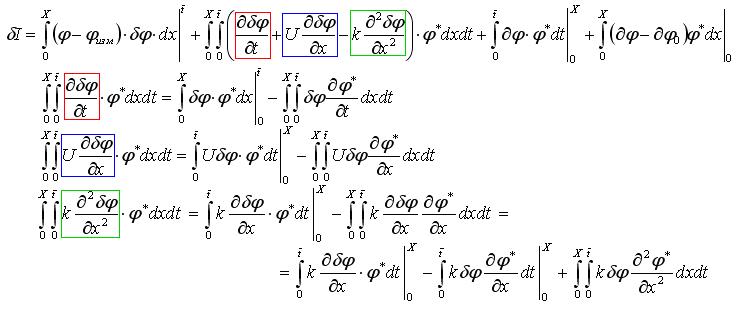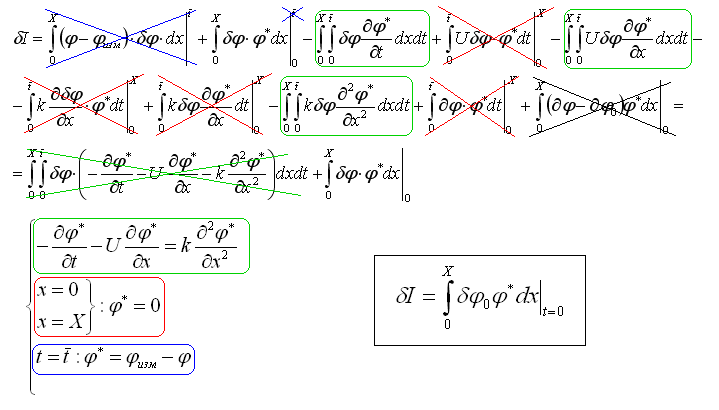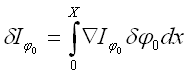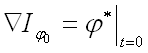Суть вариационного алгоритма усвоения данных измерений это нахождение (идентификация) таких входных параметров модели, при которых её решение наилучшим образом соответствует данным измерений. В качестве входного параметра при решении задачи усвоения рассматривается начальное поле. Такая задача называется идентификация начальных данных по данным измерений.
 

Для лучшего понимания ВАУ рассмотрим его для одномерного уравнения переноса пассивной примеси:

(1)

Пусть имеются данные измерений на конечный момент времени . Задача усвоения таких данных измерений состоит в минимизации квадратичного функционала невязок прогноза:

(2)

Минимизация такого функционала с ограничениями (связями) (1) эквивалентна минимизации следующего функционала:

(3)

где - множитель Лагранжа.

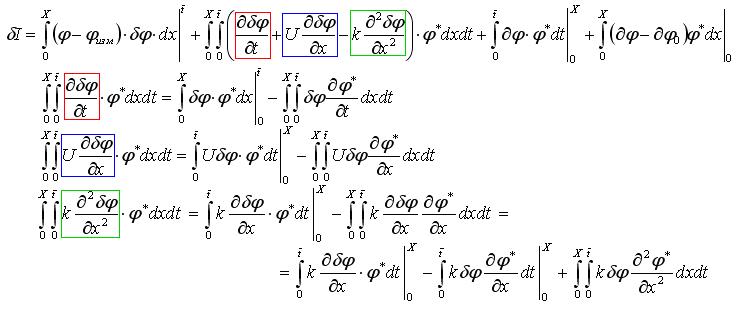(4)

решение модели варьируется только по начальным данным.

Интегрируя по частям с учетом краевых условий и выбирая пока ещё произвольные множители Лагранжа как решение следующей сопряженной задачи:

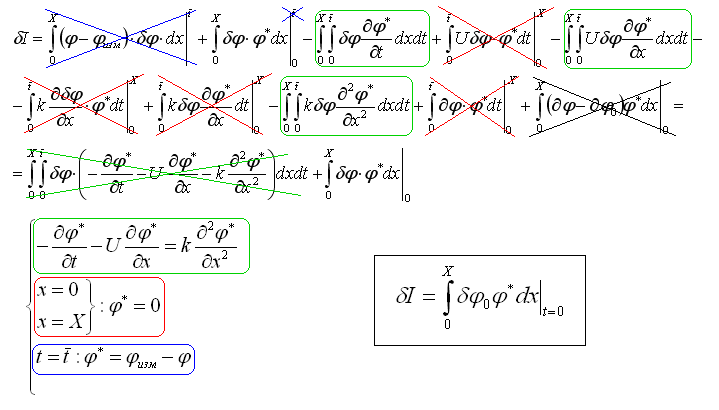(5)

Сопряженная задача является формально сопряженной к задаче (1) в смысле тождества Лагранжа, т.е. оператор сопряженной задачи является сопряженным к оператору основной задачи.

Исходя из определения вариации функционала:

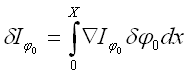Получаем достаточно простое выражение для градиента функционала по начальным данным:

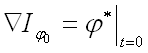(7)

Этот градиент оказывается решением построенной нами сопряженной задачи. Следующее приближение начальных данных получим путем итерационного спуска в направлении этого градиента функционала по формуле:

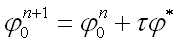(8)

где n - номер итерации,

- итерационный параметр

В процессе итераций мы инициализируем (восстанавливаем) такое начальное поле при котором решение нашей модели хорошо соответствует данным измерений.

Алгоритм идентификации в трехмерном случае является аналогичным одномерному.